Welcome to our lesson on Understanding Linkage Criteria in Hierarchical Clustering. In this lesson, we will explore the main types of linkage criteria and their roles in hierarchical clustering.
Our main objective is to explain four types of linkage criteria: Single, Complete, Average linkage, and Ward's method. We will also see how to implement these linkage criteria using R, specifically with the hclust function, which is commonly used for hierarchical clustering in R. Let's dive into the world of hierarchical clustering and linkage methods!
Hierarchical clustering is a popular method for cluster analysis in data mining, as it helps visualize how similar objects are grouped together to form clusters. At each step of hierarchical clustering, objects or clusters are merged based on a specific rule called the Linkage Criteria.
Linkage criteria determine how the distance between clusters is calculated, and this distance guides which clusters are merged at each step. Different linkage methods define cluster distance in different ways, which can significantly affect the resulting clusters.
Choosing the right linkage method can have a big impact on the shape and size of the clusters you find. Let's explore each of these linkage methods in detail!
Single Linkage, also known as the Minimal Intercluster Method, computes the distance between two clusters as the smallest distance between any point in one cluster and any point in the other cluster. In other words, single linkage looks for the shortest link or the nearest neighbor between clusters.
Single linkage can produce detailed dendrograms and handle clusters with non-elliptical shapes, but it can sometimes result in "chaining," where clusters are joined together due to a single close pair of points.
Complete Linkage, or the Maximum Intercluster Method, computes the distance between two clusters as the largest distance between any point in one cluster and any point in the other cluster.
This method focuses on the furthest points between clusters. Complete linkage tends to produce more compact and balanced clusters and is less prone to the chaining effect seen in single linkage.
Average Linkage computes the distance between two clusters as the average distance between all pairs of points, with one point from each cluster. This method provides a compromise between single and complete linkage.
Average linkage is less sensitive to noise and outliers and often produces clusters of similar diameter. However, it may favor more compact, globular clusters.
Ward's Method is different from the other linkage methods. Instead of directly measuring distances between points, it calculates the increase in the total within-cluster variance when two clusters are merged. In practice, this is often done by minimizing the sum of squared differences within all clusters.
Ward's method tends to create compact clusters of similar size and is especially useful when you want to minimize the variance within each cluster.
Let's compare the results of different linkage methods using R. We will generate synthetic data using the MASS::mvrnorm function to create four clusters, then perform hierarchical clustering with each linkage method and visualize the results. This time, we'll use a single faceted plot to compare all methods side by side.
The visualization above allows you to compare how different linkage methods can lead to different clustering results. Notice how the shape and compactness of clusters change depending on the linkage method used. Each panel shows the same data, but the clusters (colors) are assigned according to the selected linkage method. All panels share the same x and y axes for a fair comparison.
The plot above shows the results of hierarchical clustering using each of the four linkage methods: Single, Complete, Average, and Ward's. Each panel displays the same synthetic dataset, but the clusters (indicated by color) are assigned according to the respective linkage method.
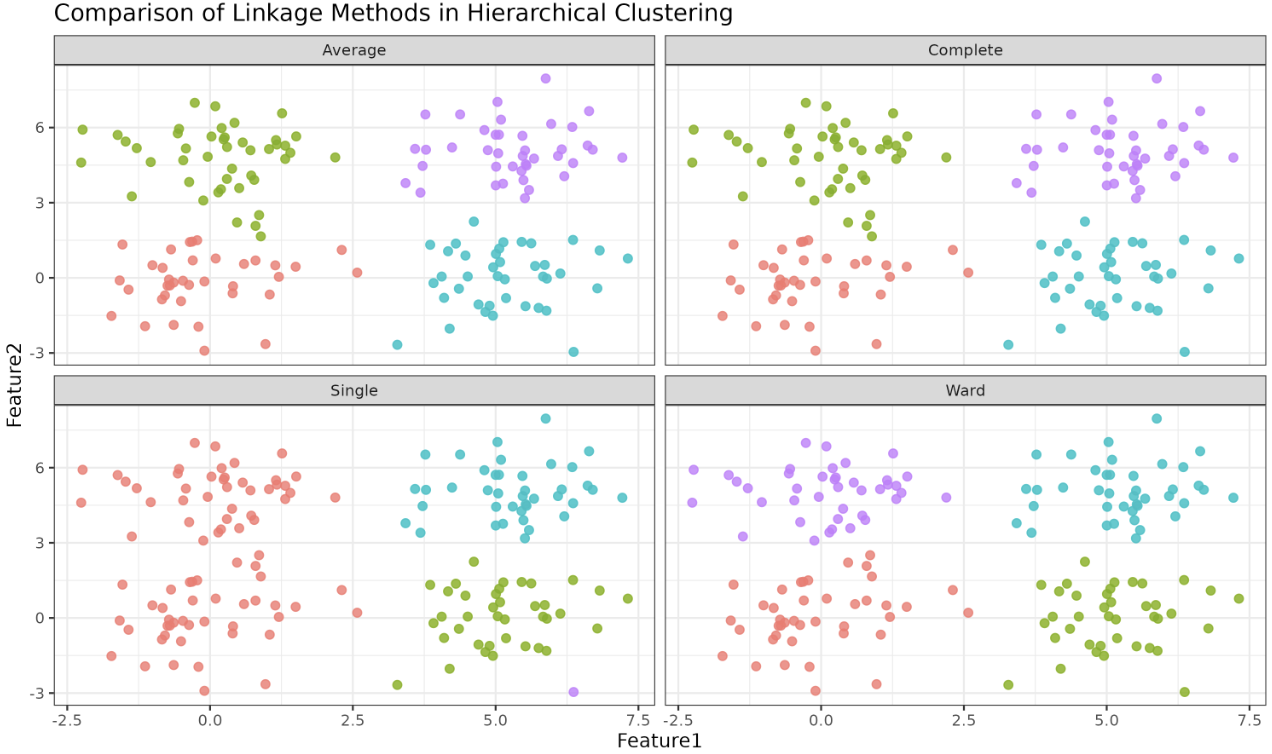
Notice how:
- Single Linkage tends to form elongated, chain-like clusters, sometimes connecting points that are only loosely related.
- Complete Linkage produces more compact and well-separated clusters, avoiding the chaining effect.
- Average Linkage offers a balance, resulting in clusters that are generally compact but not as tight as those from complete linkage.
- Ward's Method creates clusters that are very compact and similar in size, minimizing the variance within each cluster.
By comparing these panels side by side, you can clearly see how the choice of linkage method affects the shape, size, and separation of the resulting clusters. This visual comparison is a powerful tool for understanding which linkage method might be most appropriate for your data and analysis goals.
The choice of linkage method in hierarchical clustering depends on your data and the goals of your analysis.
Here are some factors to consider:
- Single Linkage: Good for capturing fine details and chain-like structures, but can produce elongated clusters due to sensitivity to outliers.
- Complete Linkage: Produces more compact and balanced clusters, is less prone to chaining, but may split large clusters.
- Average Linkage: Balances the properties of single and complete linkage, is less sensitive to noise, and often produces well-defined clusters of similar size.
- Ward's Method: Minimizes within-cluster variance, resulting in compact, uniform clusters. Best when you expect clusters to be similar in size and shape.
There is no universal best choice. The right linkage method depends on your data, your goals, and the structure you expect to find. Experimenting with different methods and visualizing the results, as shown above, can help you make an informed decision.
In this lesson, we explored four fundamental types of linkage criteria: Single, Complete, Average linkage, and Ward's method. We learned how each method works, implemented them in R using the hclust function, and visualized their effects on clustering results using a faceted plot for direct comparison. By comparing the different linkage methods, you can see how the choice of method influences the clusters you find.
Upcoming practice exercises will help you reinforce your understanding of these important concepts in hierarchical clustering. Keep experimenting with R, and enjoy your journey into data clustering!
