Distance metrics are mathematical formulas used to measure how far apart two points are. In clustering, these metrics help us determine how similar or different data points are from each other. The choice of distance metric can significantly affect the clustering results.

Euclidean distance is the straight-line distance between two points in space. It is the most common distance metric in clustering.

Formula:

Manhattan distance measures the sum of the absolute differences of their coordinates, like navigating a city grid.

Formula:

Cosine distance is based on the cosine of the angle between two vectors. It is useful for high-dimensional or text data.

Cosine Similarity Formula:

The distance metric you choose determines how the clustering algorithm groups data points. Let’s see how to use these metrics in a hierarchical clustering algorithm by first creating a flexible distance matrix function.

Distance Matrix Function:

Now, let’s use the distance matrix in an agglomerative clustering function that accepts any distance metric.

Agglomerative Clustering Function:

Let’s use the Iris dataset and scale it for clustering.

Scaling the data before clustering is important because some distance metrics, like Euclidean and Manhattan, are sensitive to the scale of the variables. If features are measured on different scales, those with larger ranges can dominate the distance calculations, leading to biased clustering results. Scaling ensures that each feature contributes equally to the distance computation. In contrast, cosine distance is less affected by the scale of the variables, as it measures the angle between vectors rather than their magnitude.

Now, cluster the data using each distance metric.

Let’s visualize how the choice of distance metric affects clustering.

Prepare Data for Plotting:

Plot with ggplot2:

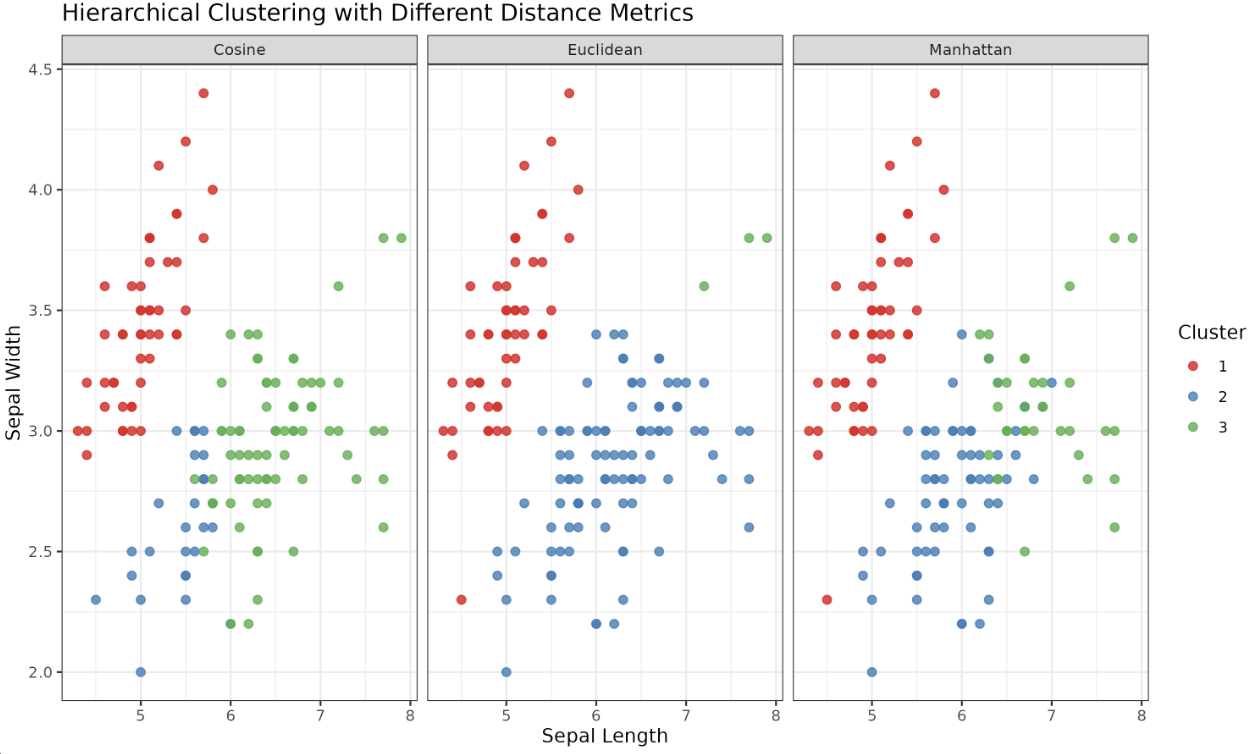
You can also use R’s built-in functions for hierarchical clustering with different distance metrics.

Euclidean and Manhattan:

Cosine Distance (Manual Calculation):

Prepare Data:

Plot:

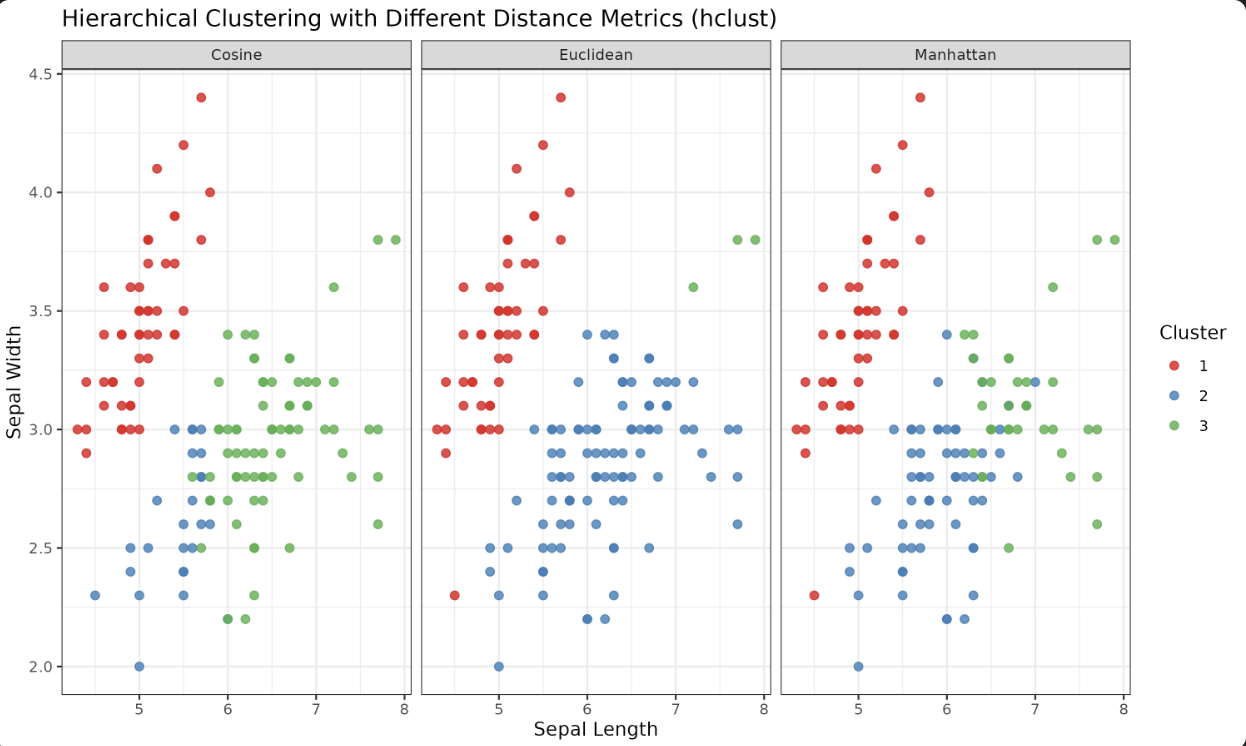
• Distance metrics define how similarity is measured in clustering.
• Euclidean, Manhattan, and Cosine distances each have unique properties and applications.
• The choice of metric can significantly change clustering results, as seen in the visualizations.

Excellent work! You've just mastered the concepts and the importance of distance metrics in hierarchical clustering. You've implemented these metrics in R and applied them in the agglomerative clustering algorithm. In the end, you studied the impact of these distance metrics on the clustering results using ggplot2 for clear and effective visualization. Next, get ready to solidify this knowledge through related exercises!