Welcome back! In the last lesson, you learned how to use different types of plots — such as histograms, bar charts, scatter plots, and boxplots — to explore the PredictHealth insurance dataset. These visualizations helped you spot patterns, compare groups, and get a general sense of how insurance charges vary across different customer profiles.

In this lesson, we will take the next step: moving from simply visualizing the data to actually quantifying the relationships between customer attributes and insurance costs. Our main goal is to discover which factors — like age, bmi, number of children, and smoking status — most strongly influence insurance pricing. You will learn how to use correlation analysis and visualization techniques to identify these key cost drivers. By the end of this lesson, you will be able not only to see patterns but also to measure and compare the strength of these relationships, setting the stage for building predictive models in future lessons.

Before we can analyze relationships, we need to make sure our data is ready. As a reminder, in previous lessons, you already checked for missing values and cleaned the dataset. Now, we will focus on selecting the most relevant numerical features for our analysis: age, bmi, children, and charges. These columns are important because they are either continuous or count data, making them suitable for correlation analysis.

Here is how you can select these columns from the insurance dataset:

This line creates a new DataFrame called numerical_data that contains only the columns we want to analyze. By narrowing our focus to these features, we can more easily interpret the results and avoid confusion from unrelated variables.

Now that we have our numerical features, we can calculate the correlation matrix. Correlation measures how strongly two variables move together. In Python, the .corr() method computes the Pearson correlation coefficient for each pair of columns. The result is a matrix where each value ranges from -1 (perfect negative correlation) to 1 (perfect positive correlation), with 0 meaning no linear relationship.

Important Note: While correlation tells us about the strength and direction of relationships between variables, it's crucial to remember that correlation does not imply causation. Just because two variables are correlated doesn't mean one causes the other. For example, if age and charges are positively correlated, this doesn't necessarily mean that getting older directly causes higher insurance costs — there could be other factors at play, such as age-related health conditions. When working with insurance data, always consider that multiple factors might influence costs, and correlation analysis helps us identify relationships that warrant further investigation.

Let's compute and display the correlation matrix:

The output will look something like this:

In this matrix, the diagonal values are always 1 because each variable is perfectly correlated with itself. The other values show the strength and direction of the relationship between each pair. For example, the correlation between age and charges is about 0.30, suggesting a moderate positive relationship: as age increases, charges tend to increase as well. The correlation between children and is much lower, indicating a weaker relationship.

While the correlation matrix gives us the numbers, it can be hard to quickly spot the strongest relationships. A heatmap is a visual tool that uses color gradients to make these patterns stand out. In a heatmap, strong positive correlations are shown in one color (such as red), strong negative correlations in another (such as blue), and weak or no correlations in neutral colors.

Here is how you can create a heatmap of the correlation matrix:

This code creates a large, easy-to-read heatmap. The annot=True argument displays the correlation values inside each cell, while the cmap='coolwarm' color scheme helps you quickly see which relationships are strong or weak. The vmin and vmax settings ensure the color scale is consistent from -1 to 1.

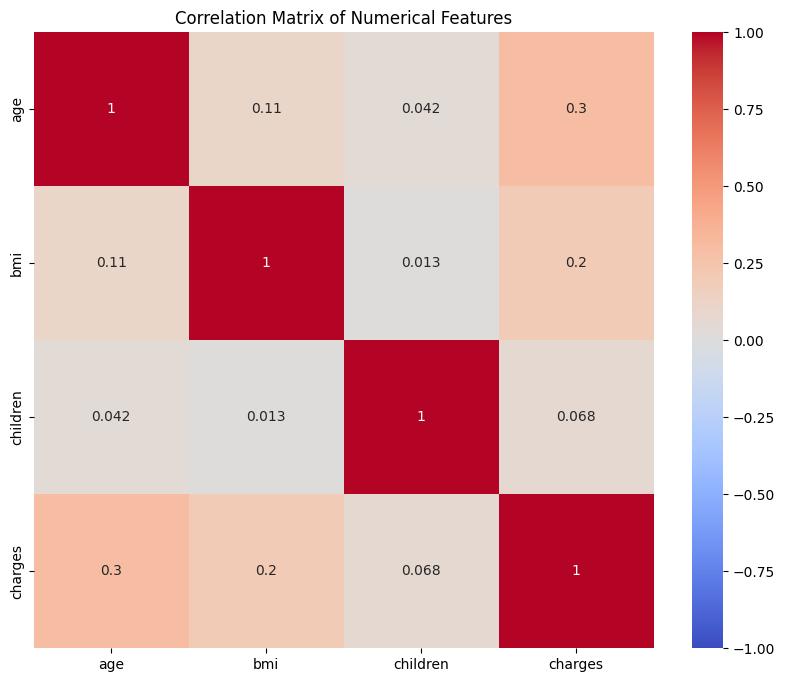
On the heatmap you can notice that the cells with the highest positive values (closer to red) indicate stronger positive relationships, while those closer to blue indicate negative relationships. For example, the cell for age and charges are a lighter color, showing a moderate positive correlation, while the cell for children and charges are closer to white, indicating a weak relationship.

To better understand how individual features relate to insurance charges, we can use scatter plots with regression lines. These plots show each customer as a point, with the x-axis representing the feature (such as age or bmi) and the y-axis representing charges. The regression line (trend line) helps you see the overall direction of the relationship.

Let’s look at two examples: age vs. charges and bmi vs. charges.

In the first plot, you can see that as age increases, insurance charges tend to rise, but there is still a lot of spread. The red regression line shows the general upward trend. In the second plot, you may notice a similar but weaker trend for bmi. Some outliers — such as customers with very high charges — may stand out, especially among those with high bmi.

These visualizations help you see not just the strength of the relationship, but also the presence of outliers or clusters that might affect your analysis.

While scatter plots are great for continuous variables, boxplots are useful for comparing distributions across groups. For example, you might want to see how insurance charges differ by the number of children or by smoker status.

Here is how you can create these boxplots:

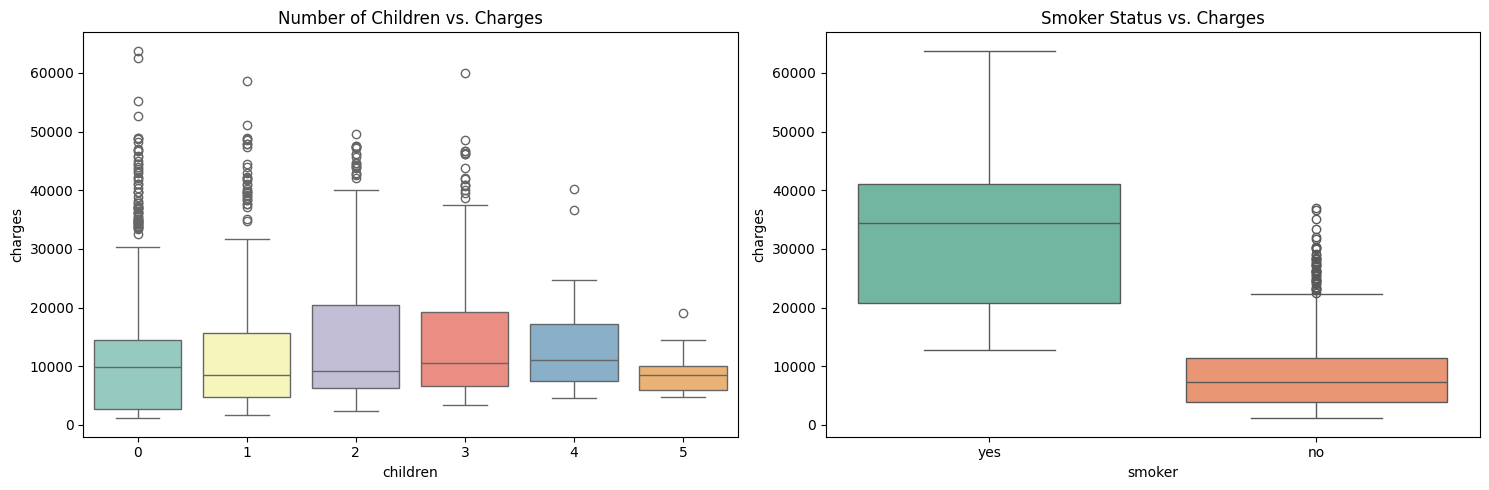
In the first boxplot, each different color represents a different number of children (0, 1, 2, 3, etc.). You can see separate boxes for customers with 0 children, 1 child, 2 children, and so on, with each category getting a distinct color from the 'Set3' palette. This makes it easy to compare the distribution of charges across different family sizes. You may notice that the median charges do not change much as the number of children increases, suggesting a weak relationship.

The second boxplot compares smokers and non-smokers, with each group getting a different color from the 'Set2' palette. This plot usually shows a dramatic difference: smokers tend to have much higher charges, and the spread is also greater, indicating more variability in costs among smokers.

To get a clearer picture, you can also look at average charges by group using summary statistics:

The output might look like this:

These results show that smoking status has a very strong effect on charges, while region and gender have smaller differences. This kind of group-level analysis helps PredictHealth understand which customer segments are most costly and why.

In this lesson, you learned how to move from simple visual exploration to quantifying and visualizing the relationships between customer attributes and insurance costs. You prepared your data by selecting key numerical features, computed and interpreted the correlation matrix, and used a heatmap to quickly spot strong and weak associations. You also explored individual relationships with scatter plots and regression lines, and compared group-level trends using boxplots and summary statistics.

These techniques are essential for identifying the main cost drivers in the PredictHealth insurance dataset. Understanding which factors most strongly influence charges will help you build better predictive models and make more informed business decisions.

You are now ready to practice these methods on your own. In the next set of exercises, you will calculate correlations, create heatmaps, and interpret group-level trends to reinforce what you have learned. If you need to review any of the code or concepts, feel free to revisit this lesson as you work through the practice problems.