Welcome to our journey into high-dimensional data and the associated challenges that it presents. We'll focus on Principal Component Analysis (PCA), a significant method in the realm of dimensionality reduction. Using a real-world example, we'll implement PCA in R. This lesson's roadmap proceeds as follows:

1. Introducing high-dimensional data and understanding its challenges
2. Establishing the need for dimensionality reduction
3. Unveiling PCA, its algorithm, and benefits
4. Implementing PCA using R

High-dimensional data describes a dataset teeming with numerous features or attributes. One good example of high-dimensional data that would benefit from Principal Component Analysis (PCA) is a dataset from a customer survey.

This dataset may have many different features (dimensions), including age, income, frequency of shopping, amount spent per shopping trip, preferred shopping time, location, and scores on several opinion and satisfaction questions, such as product variety, staff helpfulness, and store cleanliness.

If these many features all contribute relatively equally to the variance in the dataset, or if there exist correlations among these features, it might be challenging to visualize the data or draw useful conclusions directly from it. By using PCA, we can reduce the dimensionality of the dataset without significant loss of information and identify the primary areas (principal components) that explain the most variance among customers.

Let's take a look at an example where we wish to model the relationship between height and weight. In our dataset, we have three features but want to reduce the dimensionality to only two features.

In our example, we examine a dataset recording individuals' and in two different units — inches and centimeters. This redundancy increases the dimensionality of our dataset.

We show a scatter plot of height in inches versus centimeters, revealing the redundancy as the data points line up in a straight line.

Plotted Image:

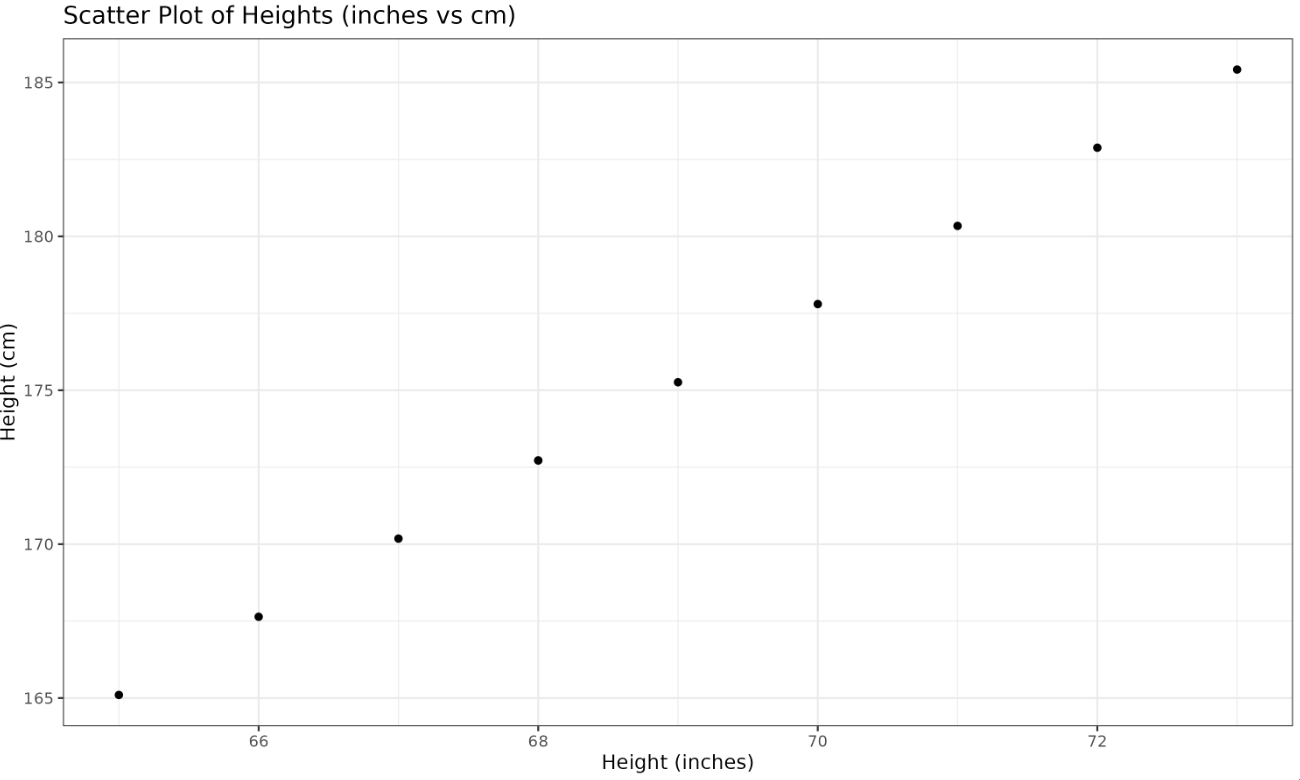
PCA is sensitive to the scale of the variables. If features are measured in different units (e.g., height in centimeters vs. weight in pounds), the feature with the largest scale will dominate the principal components. For example, in our dataset, height_cm values are much larger than height (inches) or weight_lbs, so PCA would mostly capture the variance in centimeters, ignoring the other features.

Standardization (scaling to mean 0 and standard deviation 1) ensures that each feature contributes equally to the analysis, regardless of its original unit or scale. This is why we use the scale() function before applying PCA.

When to Use Covariance Matrix vs. Correlation Matrix:

• Covariance matrix: Use when all features are measured in the same units and have similar scales.
• Correlation matrix: Use when features are measured in different units or have very different variances. The correlation matrix is equivalent to running PCA on standardized data.

In practice, standardizing the data and using the covariance matrix is equivalent to using the correlation matrix on the original data.

High-dimensional data poses numerous challenges, especially due to the curse of dimensionality causing data sparsity and consequent overfitting. With too many features, our model could perform poorly. PCA comes into play here, aiming to reduce the redundancy between the two height dimensions.

PCA is a technique that captures the dataset's primary patterns. It seeks the directions of maximum variability in the data and projects it onto a new subspace with fewer dimensions.

The steps of PCA are:

1. Standardizing the data: This process adjusts the variables to have a mean of 0 and a standard deviation of 1. This is crucial when features are on different scales or units.
2. Computing the covariance matrix: The covariance matrix represents the covariance between all pairs of features. Covariance is a measure of how much two random variables vary together.
3. Obtaining the eigenvalues and eigenvectors of the covariance matrix: The eigenvectors (principal components) represent the directions of the new feature space, and the eigenvalues explain the variance of the data along these new feature axes.
4. Sorting eigenvalues and selecting eigenvectors: The eigenvectors with the highest corresponding eigenvalues represent the best principal components.
5. Projecting the data onto the new subspace: This leads to the transformation of the original dataset to a reduced-dimensional dataset.

Let's define some functions to standardize our data and compute the covariance matrix. In R, we can use the built-in scale() function to standardize, cov() to compute the covariance matrix, and eigen() to obtain eigenvalues and eigenvectors.

We'll add print statements to help you see what's happening at each step.

Sample Output:

Let's use PCA to combine the two height features into a single principal component. We'll use ggplot2 and facet_wrap to visualize both the original data and the data after PCA side by side.

Plotted Image:

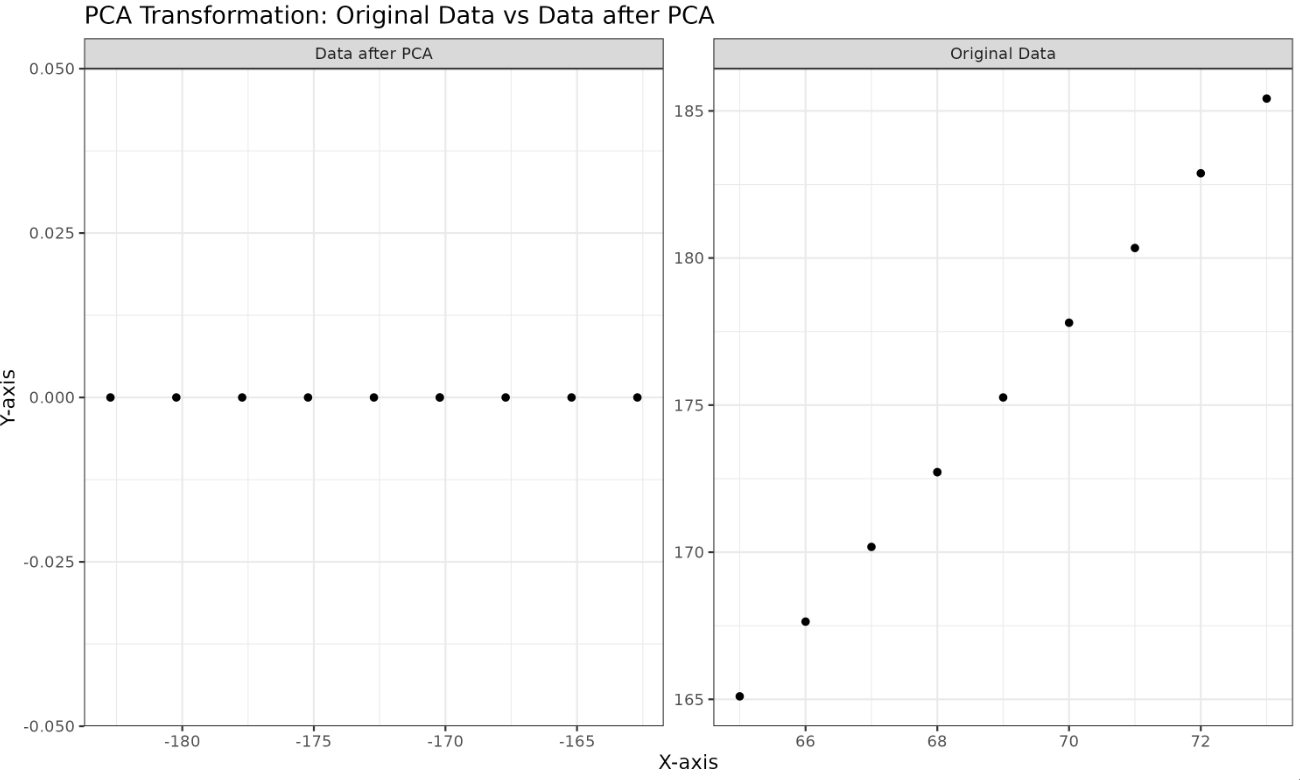
We've successfully merged two features into a single critical one while retaining essential information.

Now that we've seen how to reduce 2-dimensional data to 1-dimensional data, let's reduce our original 3-dimensional data to 2 dimensions.

Plotted Image:

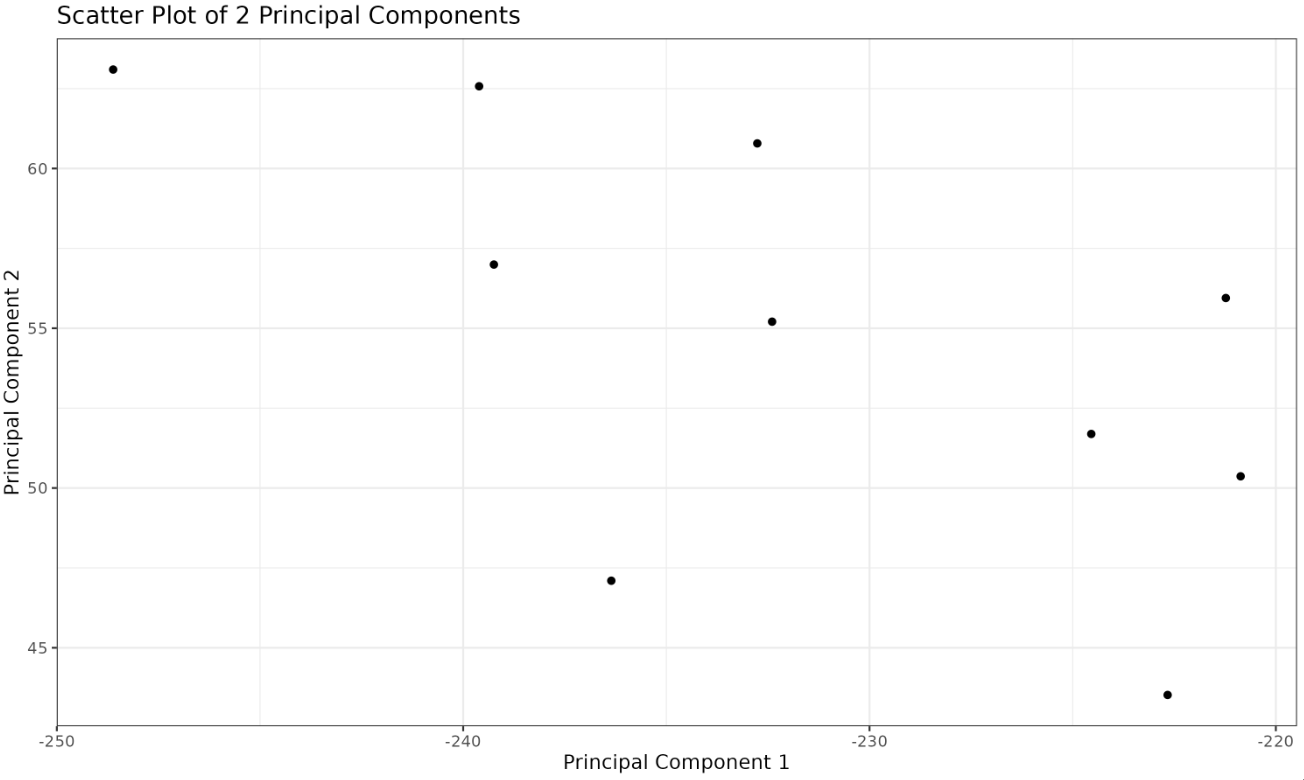
The plot successfully shows how to model our 3-dimensional data into two principal components.

Today, we unraveled high-dimensional data, its challenges, and the importance of PCA, including why scaling matters and when to use the covariance or correlation matrix. We also practically implemented PCA in R with step-by-step outputs. Coming up, we've prepared practice exercises to bolster your understanding and expertise. Let's dive deeper into the PCA cosmos! Happy coding!