Welcome to our exploration of Interpreting Principal Component Analysis (PCA) Results and its application in Machine Learning. Today, we will first generate a synthetic dataset with features inherently influenced by various built-in factors. Next, we will computationally implement PCA and explore variable interactions. We will then compare the performance of models trained using the original features and the principal components derived from PCA. Let's dive right in!

Incorporating PCA-reduced data into Machine Learning models can significantly enhance our model's efficiency and lessen the issue of overfitting. PCA aids in reducing dimensionality without losing much information. This feature becomes increasingly useful when we deal with real-life datasets that have numerous attributes or features.

Our first step is to create a synthetic dataset, which consists of several numeric features that naturally influence each other. The purpose of including these dependencies is to later determine if PCA can detect these implicit relationships among the features.

Note: In this example, the feature monthly_calls is generated as monthly_calls <- 100 + 2 * tenure + 0.5 * data_usage, which is a nearly exact linear combination of tenure and data_usage (with no added noise). This makes the dataset less realistic, but it helps illustrate how PCA can identify and handle such linear dependencies.

Now, let's put our data into a data frame:

This portion of the code generates random variables to simulate typical customer usage data. This includes usage facts such as monthly_charges, , and , and a binary variable that is influenced by these features. All this data is assembled together in a data frame.

Before we can proceed to PCA, it's necessary to scale our features using standardization. Additionally, we also need to perform a train-test split of our data.

Note: Here, scaling is performed on the entire dataset before splitting into training and test sets. In a real-world scenario, it is best practice to fit the scaler on the training data only and then apply it to the test data to avoid data leakage. For simplicity in this example, we scale the whole dataset first.

Data scaling is necessary for PCA because it is a variance-maximizing exercise. It projects your original data onto directions that maximize the variance. Thus, we need to scale our data so that each feature has unit variance.

With the data prepared, let's apply PCA and evaluate its results.

Note: Since X_train is already scaled, we set center = FALSE and scale. = FALSE in prcomp().

When interpreting PCA, two key metrics help us understand how much information (variance) each principal component captures from the original data:

• Explained Variance Ratio: This shows the proportion of the dataset’s total variance that is explained by each individual principal component. It helps us see which components carry the most information and is typically visualized using a scree plot.
• Cumulative Explained Variance: This is the running total of the explained variance as we add more principal components. It helps us determine how many components are needed to capture a desired amount of the total variance (for example, 95%).

In practice, we look at both the explained variance ratio and the cumulative explained variance to decide how many principal components to retain. Below, we will visualize both metrics using separate plots.

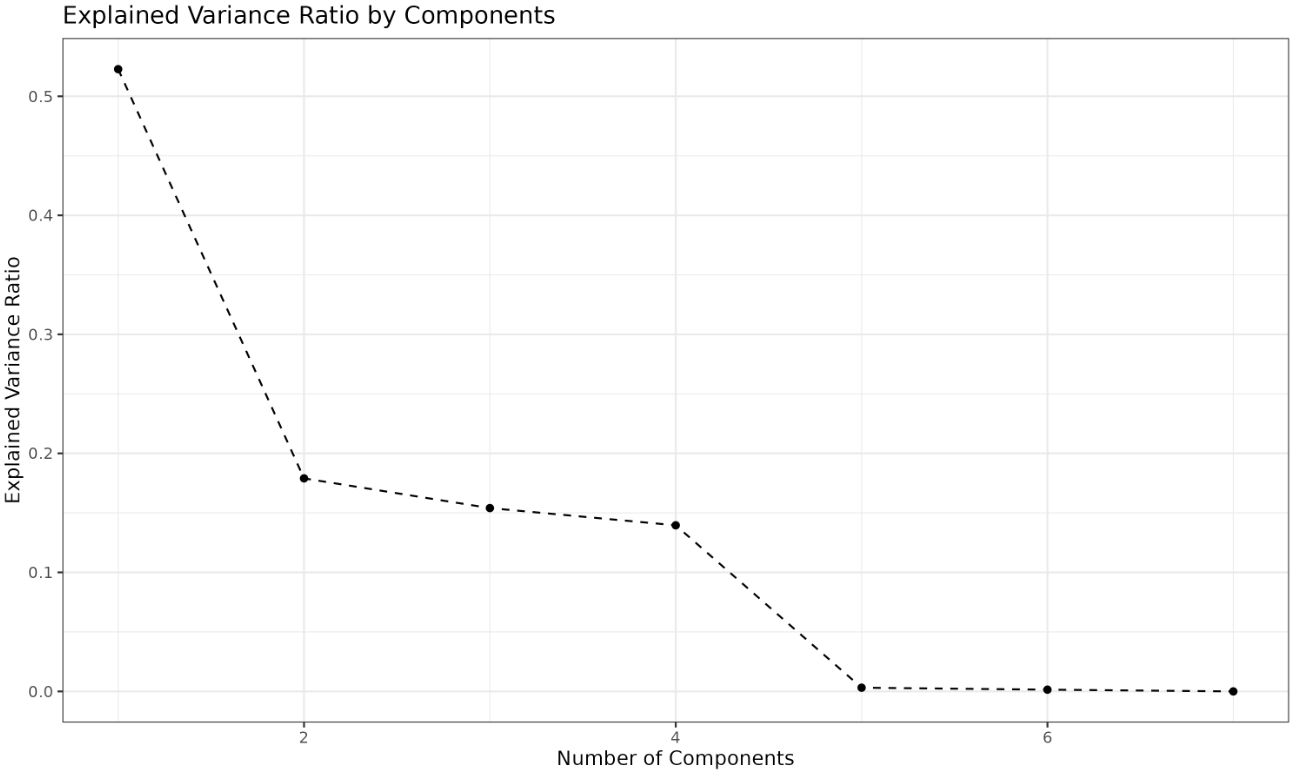
The scree plot displays how much variance each principal component explains. Each point on the plot represents a principal component, and its height shows the proportion of the total variance captured by that component. Typically, the first few components explain most of the variance, and the remaining components contribute less. The "elbow" point—where the plot starts to flatten—indicates that adding more components beyond this point yields diminishing returns in terms of explained variance. This helps you decide how many components are worth keeping.

Output:

The cumulative explained variance plot shows the total variance explained as you add more principal components. Each point represents the sum of the explained variances up to that component. This plot helps you determine the minimum number of components needed to reach a desired threshold of total variance (such as 95%). For example, if the curve crosses 0.95 at the fourth component, you know that the first four components together explain at least 95% of the variance in your data. This is a practical way to balance dimensionality reduction with information retention.

Output:

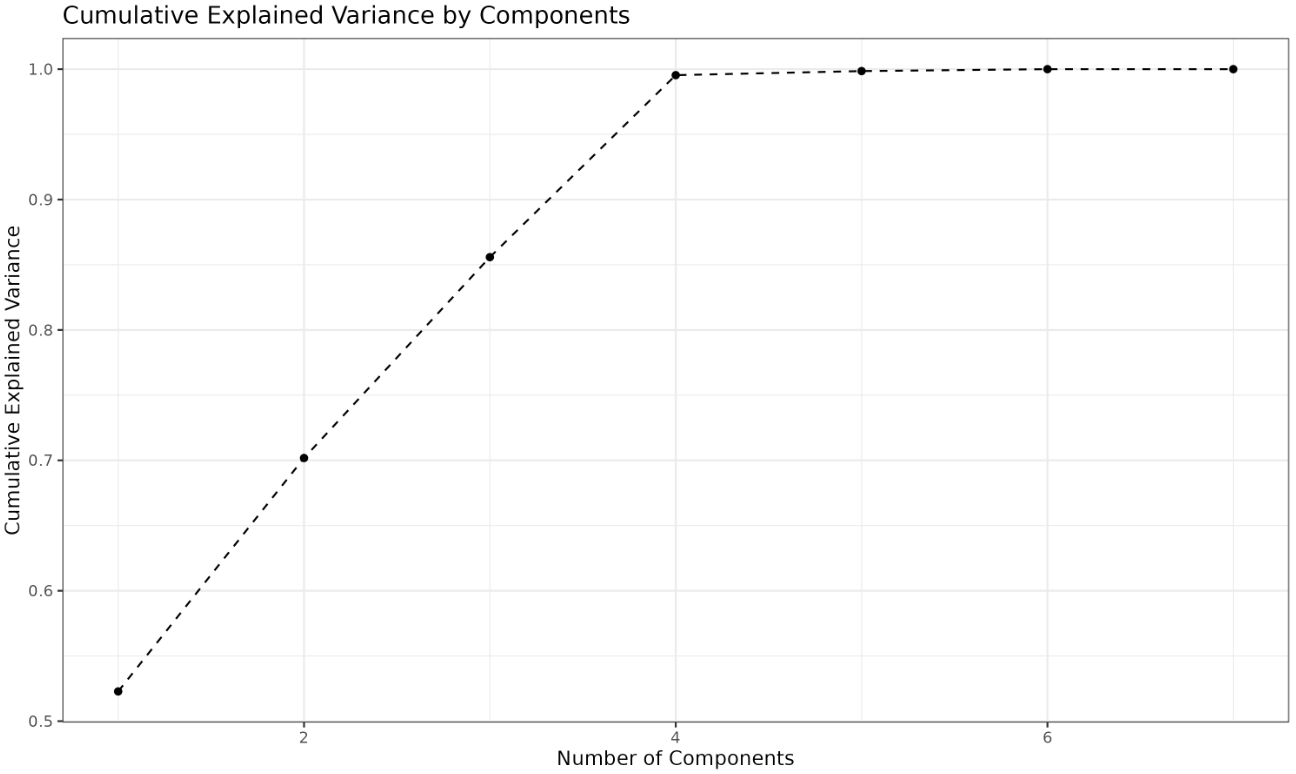
Now, let's use the cumulative explained variance to decide on the number of principal components to retain.

This part of the code calculates the number of principal components needed to retain at least 95% of the original data's variance.

Finally, we will train logistic regression models on both sets of data and compare them.

The accuracy of a model trained on PCA-transformed data is computed.

The accuracy of a model trained on the original data without PCA transformation is also calculated for comparison. Notice that both models may have the same accuracy score, indicating that PCA did not affect the model's performance but reduced the number of features, thereby simplifying the model.

We have successfully covered creating a synthetic dataset, preparing the data, implementing PCA, visualizing both the explained variance ratio and cumulative explained variance, determining the number of principal components to retain, and comparing the accuracies of models trained with and without PCA. In the next lesson, we'll delve deeper into PCA and other dimensionality reduction techniques. Happy learning!