Welcome to the world of Linear Discriminant Analysis (LDA), a technique widely used for dimensionality reduction in supervised learning. In this lesson, we'll explore the concepts behind LDA and build an implementation from scratch using R. For our practical example, we'll use the classic Iris dataset, a well-known dataset in R, to demonstrate how LDA works in practice.

LDA reduces dimensionality by constructing a feature space that optimally separates the classes in the data. The axes in this space are linear combinations of the original features and are known as eigenvectors. The LDA algorithm consists of several steps, such as calculating class mean vectors and scatter matrices, then finding eigenvalues and eigenvectors that map the original feature space onto a lower-dimensional space.

To understand LDA, let's start with a simple two-dimensional example. Suppose we have data points scattered across a 2-D space, with each point belonging to one of two possible classes.

In LDA, we want to project these points onto a line such that, when the points are projected, the two classes are as separated as possible. The goal here is twofold:

1. Maximize the distance between the means of the two classes.
2. Minimize the variation (in other words, the scatter) within each category.

This forms the intuition behind LDA. The crux of an LDA transformation involves formulating a weight matrix and transforming our input data by multiplying it with this weight matrix. The weights here help increase class separability. Let's see how we can achieve this mathematically using scatter matrices.

Scatter matrices are a critical part of LDA. To understand them, we need to differentiate between two types of scatter matrices:

1. The within-class scatter matrix measures the variability of data points within each class.
2. The between-class scatter matrix captures the variability between different classes.

Mathematically, the within-class scatter matrix $S_W$ is computed as the sum of scatter matrices for each class, and the between-class scatter matrix $S_B$ is calculated based on the means of different classes.

Given the mathematical foundations of within-class and between-class scatter matrices, the steps involved in the LDA algorithm can be conceptualized as:

1. Compute class means: Calculate the average value for each class.
2. Compute the within-class scatter matrix $S_{W}$.
3. Compute the weights that maximize separability: This is obtained by multiplying the inverse of $S_{W}$ and the difference between the class means.
4. Use the weights to transform our input data.

Let's load the Iris dataset for LDA, which is a 3-class dataset with 4 features. In this example, we'll rename the features to weight_lbs, weight_kgs, and height for demonstration purposes.

Before proceeding, it's important to consider whether to scale your data for LDA. LDA makes the assumption that each class shares the same covariance structure, and the method is sensitive to the scale of the input features. If your features are measured in different units or have very different variances, those with larger scales can dominate the computation of scatter matrices and the resulting discriminant directions. This can lead to misleading results, as LDA may focus on the features with the largest variances rather than those that best separate the classes.

When to scale:

• If your features are on very different scales (e.g., height in centimeters and weight in kilograms), scaling is recommended.
• If all features are already on a similar scale, scaling may not be necessary.

How to scale:
A common approach is to standardize each feature to have zero mean and unit variance. This ensures that each feature contributes equally to the analysis, and the LDA solution is not biased toward features with larger variances.

Let's standardize the features in our example:

By scaling the data, we help ensure that LDA's assumptions are more closely met and that the resulting discriminant axes are not unduly influenced by the scale of any particular feature.

In R, instead of classes, we typically use lists and functions to encapsulate model state and behavior. We'll define a list to hold the transformation matrix and functions to perform the LDA steps.

Here, LDA is a list that will store the transformation matrix W after fitting the model.

The within-class scatter matrix is a crucial component in the LDA algorithm — it encapsulates the total scatter within each class. To calculate it, we first define the scatter matrix for each class, and then add them all to give us the within-class scatter matrix, $S_{W}$.

Mathematically, the scatter matrix for a specific class is computed via:

The between-class scatter matrix captures the variance between different classes. It is calculated as follows:

Now that we've calculated the scatter matrices, we can write a function to fit the LDA model. This function finds the generalized eigenvalues and corresponding eigenvectors, and selects a subset for transformation.

The function above computes the eigenvalues and eigenvectors of the matrix $S_W^{-1}S_B$, sorts them by eigenvalue, and selects the top eigenvectors to form the transformation matrix .

Next, we fit the LDA model, transform the data, and plot the projected samples using ggplot2. We'll use the first two components for visualization.

The output will look like this:

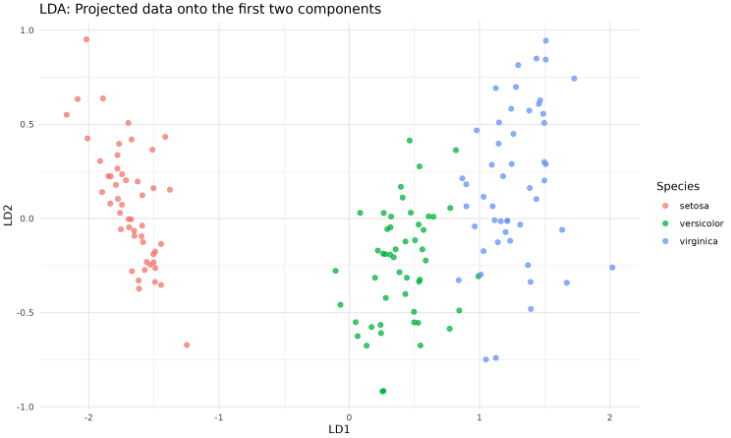
This code creates a scatter plot of the data projected onto the first two linear discriminants, colored by species.

Great job! You've successfully understood the concepts of LDA and its mathematical foundation, and built a simple LDA from scratch using R. Now, get ready for practice exercises to apply your newly acquired knowledge and consolidate your learning! Happy learning!