Greetings! Our journey into K-means clustering deepens as we explore two crucial elements: the selection of the number of clusters and the initialization of centroids. Our aim is to comprehend these aspects and put them into action using R. Let's move forward!

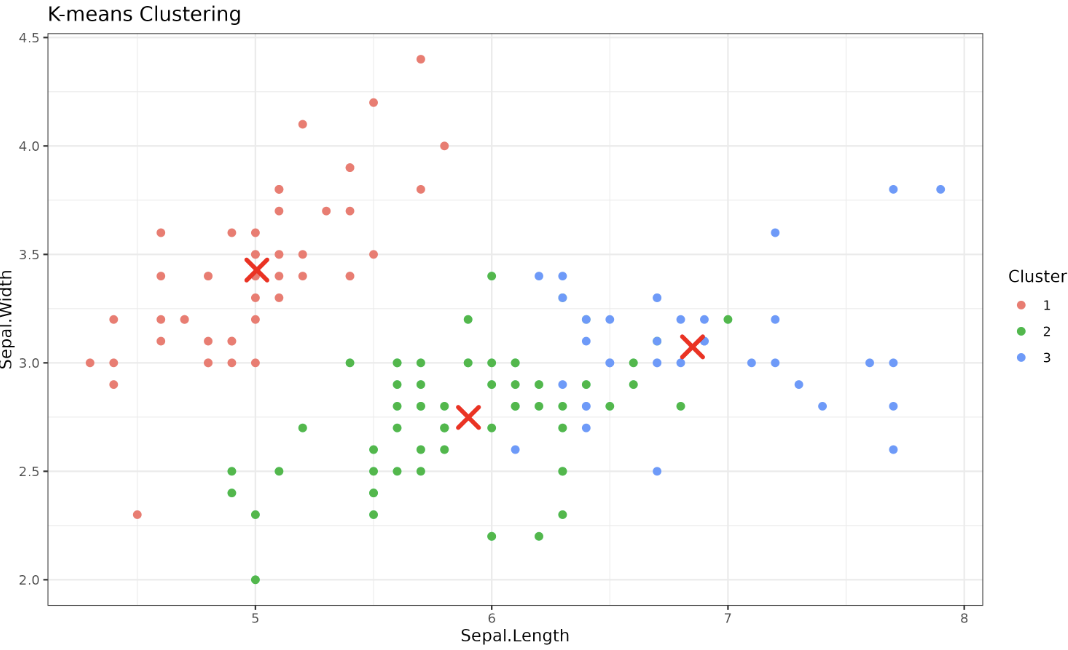
The K in K-means signifies the number of clusters. Centroids, the centers of each cluster, are equally significant. Their initial placement in K-means is crucial. Poorly initialized centroids can lead to suboptimal clustering — which is why multiple runs with different initial placements are essential. This highlights the importance of choosing both the number of clusters and their initial centroids.

R’s built-in kmeans() function allows us to specify the number of clusters and also to set the initial centroids manually. Let’s see how we can do this in R using ggplot2 for visualization.

The iter.max parameter in the kmeans() function controls the maximum number of iterations the algorithm will perform before stopping. In the example above, we set iter.max = 100 to allow the algorithm up to 100 iterations to converge. Typically, K-means converges much sooner, but setting a higher value ensures the algorithm has enough opportunity to find stable clusters, especially for more complex datasets. If the algorithm converges before reaching this limit, it will stop early. If you set iter.max too low, the algorithm might stop before finding a good solution; if you set it very high, it may just take a bit longer to run but won't affect the final result once convergence is reached.

As we've seen, different initial centroids and different choices for the number of clusters can lead to different results. R’s kmeans() function uses random initialization by default, which means the starting positions of the centroids are chosen randomly from the data. To reduce the risk of poor clustering due to unlucky initialization, you can use the nstart parameter to run the algorithm multiple times with different random initializations and select the best result. This helps mitigate the impact of poor initial centroid placement.

Let’s explore how the choice of the number of clusters affects the results of K-means clustering. We’ll use a simple 2D dataset for illustration.

This approach uses facet_wrap() from ggplot2 to display the two clustering results side by side, without requiring any extra packages. The plot is assigned to p_kmeans_k. Here is the output:

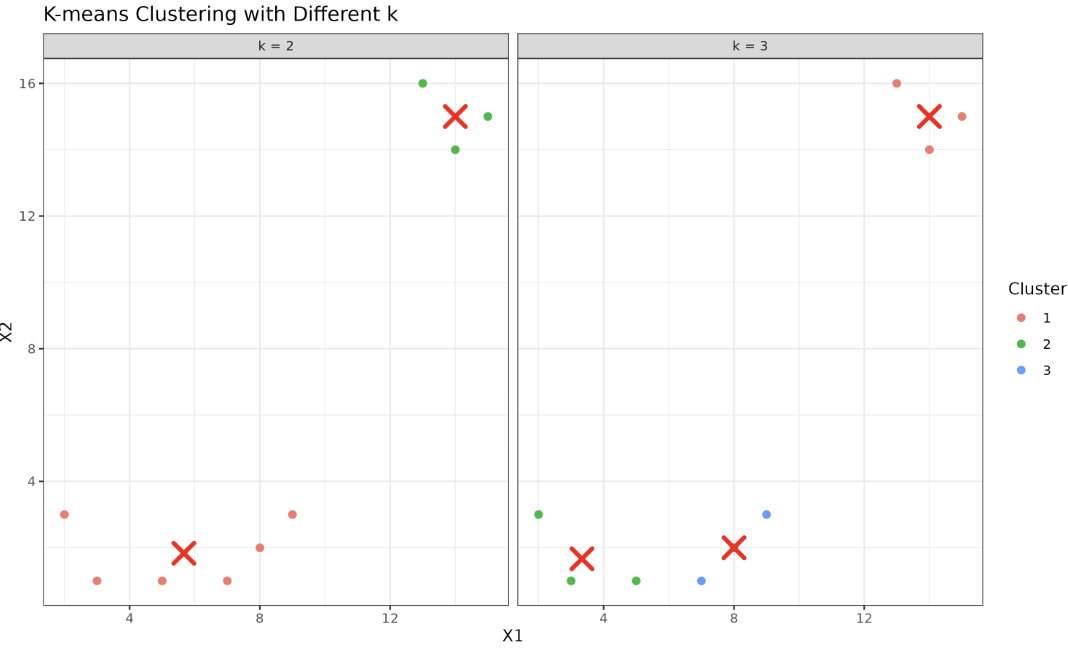
These examples illustrate the significant role the number of clusters plays in forming the final clusters. We must carefully choose this number to accurately represent the underlying structure of our data. An incorrect number of clusters could lead to overfitting or underfitting, both of which could misrepresent your data.

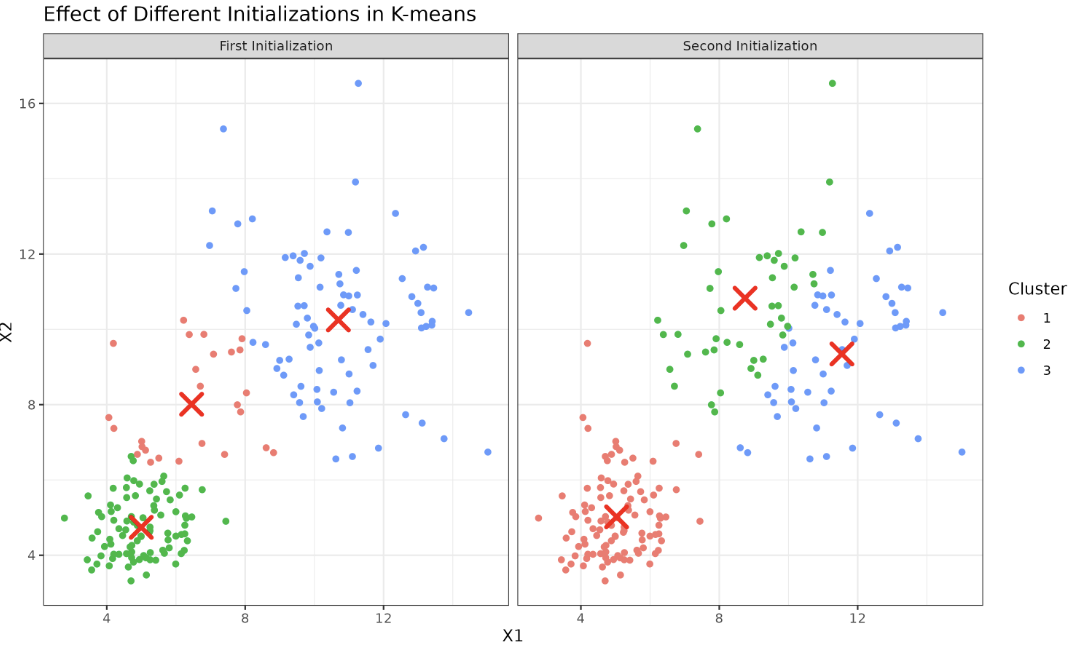
You may wonder, "Why can the initial centroid placement result in different clustering results?" The K-means algorithm is an iterative procedure that minimizes the within-cluster sum of squares. However, it only guarantees finding a local minimum, not a global one. This means that different starting positions can lead to distinct clustering outcomes.

To visualize this, imagine you're blindfolded in a hilly region where you're tasked with finding the lowest point. By feeling the ground slope, you move downward. But when there are many valleys (local minima), your starting position influences which valley (local minimum) you'll end up in — and not all valleys are equally deep. Initial centroids in K-means are akin to starting positions.

Let’s illustrate the effect of different initial centroids using a simple custom K-means implementation in R. This will help us see how sensitive the results can be to the initial choice.

In this lesson, we explored the principles of choosing the number of clusters and initializing centroids in K-means, all within the R environment. You learned how to set the number of clusters, specify initial centroids, and visualize the results using ggplot2. You also saw how different choices can affect the outcome of clustering. Practice these concepts to deepen your understanding and master K-means clustering in R.