Welcome back to 3D Worlds and Matrix Transformations! Having completed four foundational lessons, we've mastered individual transformations and can now render true 3D objects with realistic perspective projection. Our colorful cube spins gracefully in 3D space, but real-world animations often require much more complexity: objects that simultaneously rotate around their own axes while orbiting other points, scaling up and down rhythmically, or performing intricate dance-like movements through space.
In this fifth lesson, we'll explore transformation composition: the art of combining multiple transformation matrices to create sophisticated, multi-layered animations. We'll take our spinning cube and transform it into a complex animated system that performs self-rotation, orbital motion, and rhythmic scaling all at the same time. By understanding how different transformations work together and why their order matters critically, we'll unlock the ability to create rich, engaging 3D animations that captivate viewers with their complexity and fluidity.
While single transformations like rotation or translation create basic animations, real-world objects rarely move in such simple patterns. Consider a planet in our solar system: it rotates around its own axis while simultaneously orbiting the sun, and its distance from the sun might vary, creating an elliptical path. Each of these motions represents a different transformation that must work together harmoniously.
Transformation composition allows us to combine multiple transformation matrices into a single, unified transformation that captures all these complex behaviors. Rather than applying transformations sequentially in separate rendering passes, we mathematically combine them on the CPU before sending the result to the GPU as a single model matrix.
This approach is both computationally efficient and conceptually powerful: we can think about each type of motion independently (self-rotation, orbital motion, scaling), while the mathematics automatically handles their complex interactions. The key insight is that matrix multiplication allows us to "layer" transformations, creating sophisticated animations from simple building blocks.
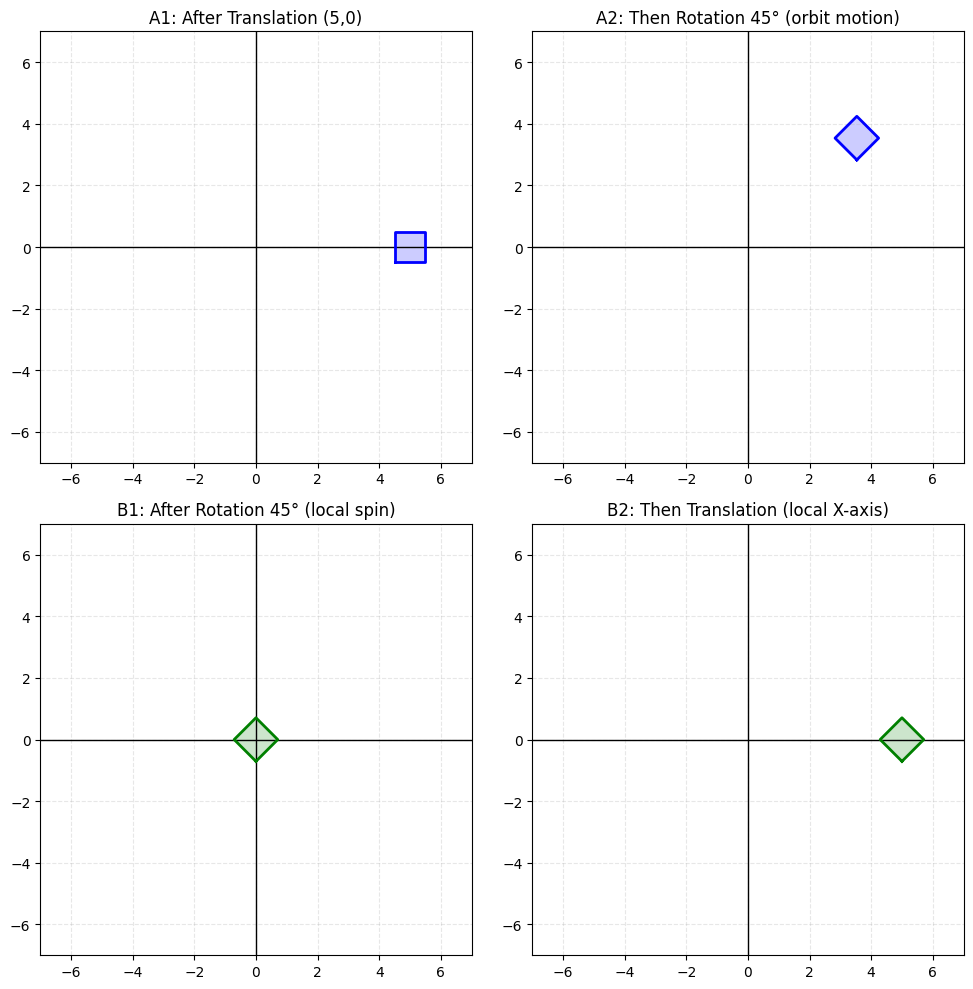
The mathematical foundation of transformation composition lies in matrix multiplication, but there's a crucial detail that often trips up beginners: matrix multiplication is not commutative, meaning that the order of operations dramatically affects the final result.
When we write , the transformations are applied from right to left: is applied first, then is applied to the result, and finally is applied to that result. This right-to-left evaluation order means that the rightmost matrix affects the object in its local coordinate system, while leftmost matrices affect the object in increasingly global coordinate systems.
Let's begin building our complex animation by implementing self-rotation: making our cube spin around its own center axis while maintaining its position in world space. This creates the familiar spinning motion we've seen before, but now it will be just one component of a larger animation system.
Our self-rotation uses currentTime * 2.0f as the rotation angle, creating a rotation speed of 2 radians per second. The rotation axis (1, 1, 0) creates an interesting diagonal spin that shows off the cube's different faces as it rotates, making the animation more visually engaging than simple axis-aligned rotation.
Since this transformation will be applied first (rightmost in our final multiplication), it affects the cube in its local coordinate system, causing it to spin around its own center regardless of any other transformations that might move or scale it.
Next, we'll add a pulsing scale effect that makes our cube stretch and compress rhythmically along its Z-axis, creating a squashing animation that adds dynamic deformation to our spinning cube.
The scaling factor uses non-uniform scaling: the X and Y axes remain at scale 1.0 (unchanged), while the Z-axis oscillates with 0.5f + 0.3f * sin(currentTime * 3.0f), which varies between 0.2 and 0.8 over time. This creates a squashing and stretching effect along the cube's depth, making it appear to compress and expand like an accordion while maintaining its width and height.
The frequency multiplier of 3.0 makes the pulsing happen 3 times faster than our basic time progression, creating a rapid squashing rhythm that adds dramatic deformation to our spinning cube. This transformation will be applied after self-rotation but before any positional changes, so the cube deforms around its own center while it spins.
To create orbital motion, we need to position our cube away from the world origin before applying any rotational movements that will swing it around that center point. This translation establishes the orbital radius of our animation.
The translation vector (2.5, 0, 0) moves our cube 2.5 units away from the origin along the positive X-axis. This creates the radius of our orbital motion: when we later apply rotational transformations around the origin, the cube will swing in a circle of radius 2.5 units.
This translation is applied after scaling and self-rotation, so it moves the already-spinning, already-pulsing cube to its orbital position. The cube maintains all its previous behaviors while now being positioned for orbital motion around the world center.
The final piece of our transformation puzzle is orbital rotation: rotating the entire scene around the world origin to make our cube trace a circular path through space while maintaining all its other behaviors.
Our orbital rotation uses a slower angular velocity (currentTime * 0.8f) than the self-rotation, creating a pleasing relationship between the fast local spinning and the slower orbital motion. The rotation axis (0, 1, 0) creates orbital motion in the XZ-plane, like a planet orbiting the sun when viewed from above the solar system.
This transformation is applied last (leftmost in our multiplication chain), so it affects the cube in its final world position: the cube self-rotates, scales, moves to its orbital position, then the entire system rotates around the origin.
Now we can combine all four transformations into a single model matrix that captures our complete animation system. The order of multiplication is critical for achieving the desired visual effect.
Reading from right to left, this transformation chain applies: self-rotation first (the cube spins around its local center), then scaling (the spinning cube squashes and stretches along its Z-axis), then translation to orbit (the deforming, spinning cube moves away from the origin), and finally orbital rotation (the entire system rotates around the world origin).
This specific order creates a cube that spins on its axis while squashing rhythmically in depth as it orbits around a central point. Changing the order would create completely different animations: for example, placing orbital rotation before translation would make the cube orbit around its own center rather than around the world origin.
Our animation system uses coordinated timing with different frequencies for each transformation type, creating complex visual rhythms that keep the animation interesting without being chaotic or unpredictable.
The self-rotation frequency of 2.0 creates rapid spinning that emphasizes the cube's three-dimensional nature. The scaling frequency of 3.0 produces quick squashing and stretching that adds dramatic deformation to the cube's geometry. The orbital frequency of 0.8 creates slow, stately circular motion that provides a stable foundation for the more rapid local animations.
These frequencies were chosen to create harmonic relationships: the self-rotation completes 2.5 full turns during each complete orbit (2.0/0.8 = 2.5), while the scaling completes 3.75 full squash-stretch cycles per orbit (3.0/0.8 = 3.75). These non-integer relationships ensure that the animation has a long period before repeating exactly, maintaining visual interest over extended viewing.
We've successfully mastered the art of transformation composition, combining multiple matrix transformations to create sophisticated, multi-layered animations that far exceed what any single transformation could achieve alone. By understanding matrix multiplication order and carefully coordinating different animation frequencies, we've created a complex orbital animation system that showcases self-rotation, scaling, translation, and orbital motion working together in perfect harmony.
This lesson represents a significant advancement in our 3D graphics capabilities: we can now create rich, engaging animations that capture viewers' attention through their complexity and fluid beauty. The principles we've learned about transformation composition and timing coordination form the foundation for virtually all advanced character animation, particle systems, and procedural motion in modern 3D graphics. The upcoming practice exercises will give you hands-on experience with these powerful animation techniques, allowing you to explore and experiment with the transformation systems we've constructed together.