Welcome back to our course Neural Network Fundamentals: Neurons and Layers! In this third lesson, we're building upon what you learned in our previous lesson about the basic artificial neuron. You've already implemented a simple neuron that computes a weighted sum of inputs plus a bias.

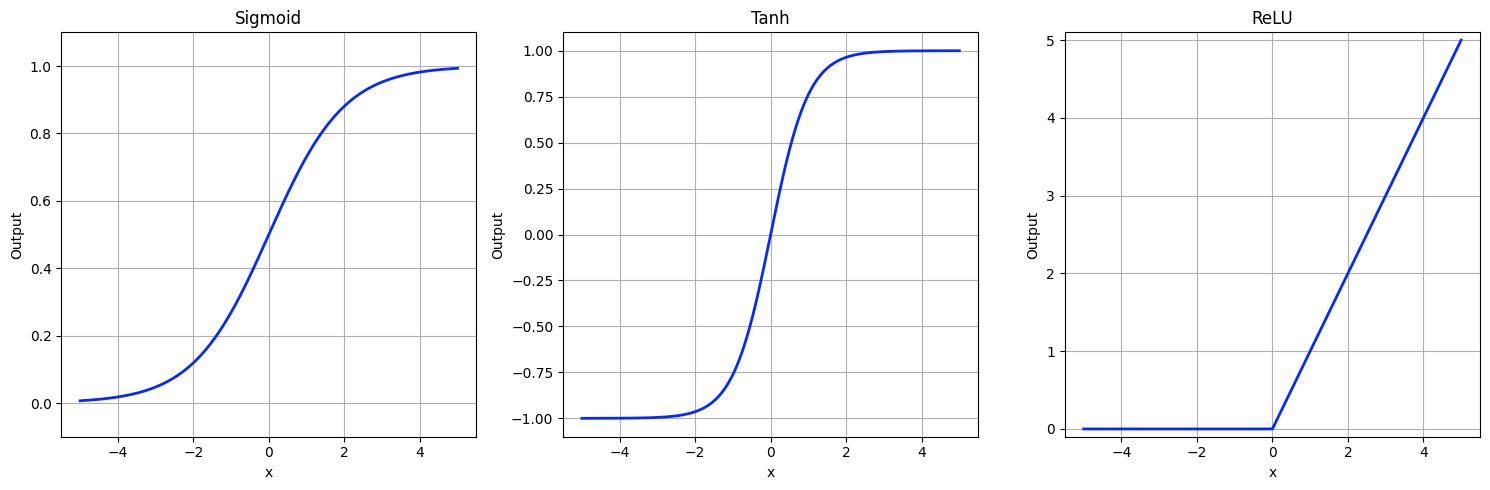
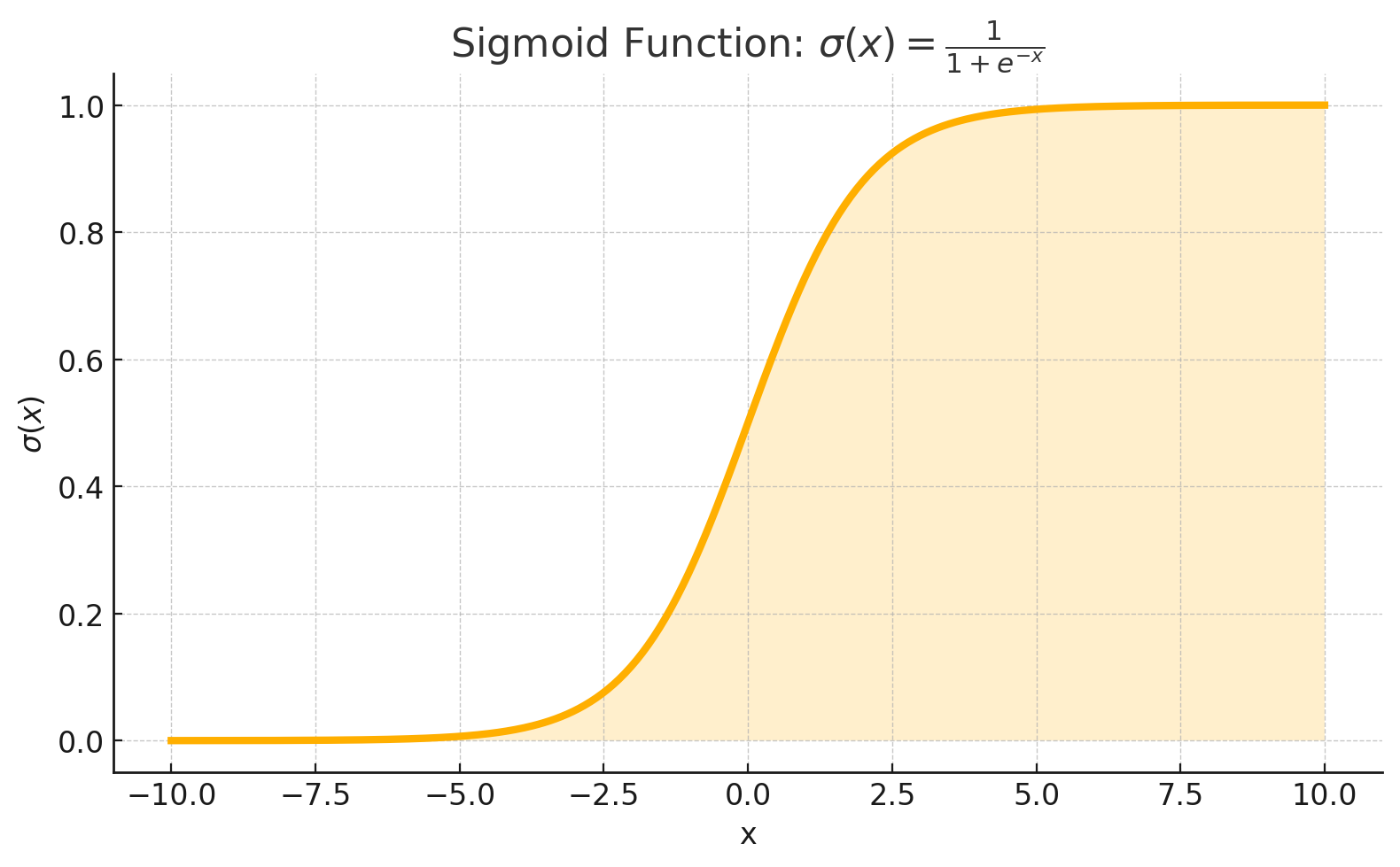
Today, we're taking an important step forward by introducing activation functions — a crucial component that enables neural networks to learn complex patterns. In particular, we'll focus on the Sigmoid activation function, one of the classical functions used in neural networks.

In our previous lesson, our neuron could only produce linear outputs. While this is useful for some tasks, it severely limits what our neural networks can learn. Today, we'll overcome this limitation by adding non-linearity to our neurons, allowing them to model more complex relationships in data.

Before diving into specific activation functions, let's understand why we need them in the first place.

The neuron we built in the previous lesson computes a weighted sum of inputs plus a bias. This is a linear transformation — mathematically, it can only represent straight lines (in 2D) or flat planes (in higher dimensions).

Consider what would happen if we stacked multiple layers of these linear neurons:

Layer 1's output is a linear function of the input: