Welcome to 3D Worlds and Matrix Transformations! We're embarking on an exciting journey into the mathematical foundations that power modern 3D graphics. In this first lesson, we'll explore one of the most fundamental concepts in computer graphics: how we use matrices to move and rotate objects in 3D space.

Today, we'll focus on understanding translation and rotation matrices. By the end of this lesson, we'll have built a solid theoretical foundation that will prepare us for the hands-on work ahead. Think of this as laying the groundwork for everything we'll create together in this course.

Before we dive into matrices, let's establish our foundation in 3D space. In computer graphics, we work with two essential mathematical objects: positions and vectors.

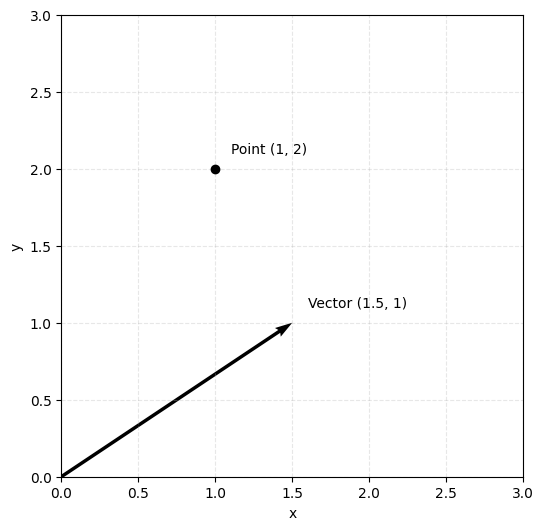
A position represents a specific point in 3D space using three coordinates $(x, y, z)$. For example, the point $(3, 5, 2)$ tells us exactly where something is located. A vector, on the other hand, represents a direction and magnitude. Think of it as an arrow pointing from one place to another, like moving 2 units right, 3 units up, and 1 unit forward, which we'd write as the vector $(2,3,$.

To truly understand how matrices transform 3D space, we need to grasp the concept of a basis. A basis is a set of vectors that defines our coordinate system—think of it as the fundamental "rulers" we use to measure and describe positions in 3D space.

The standard basis in 3D consists of three unit vectors:

• i = $\begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$ (points along the x-axis)

Here's why bases are so fundamental for linear algebra and computer graphics. Imagine you're directing an animated movie and have spent months perfecting a complex 3D scene. Every character position, every camera angle, every light source has been meticulously placed using coordinates in your standard coordinate system. Now you want to rotate the camera 45 degrees to view the scene from a different perspective.

Without a change of basis, you'd need to manually recalculate and update every single coordinate—a computational nightmare.

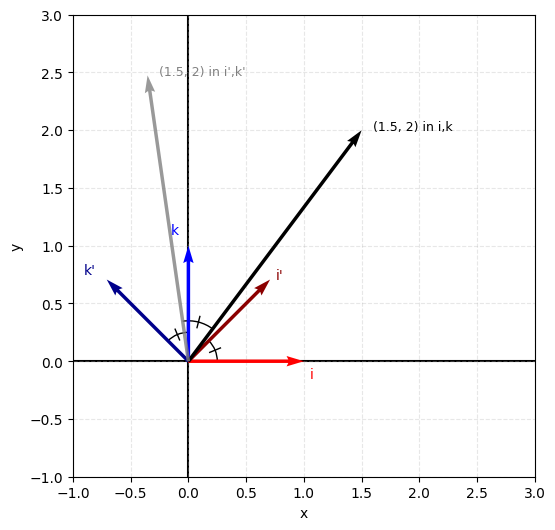
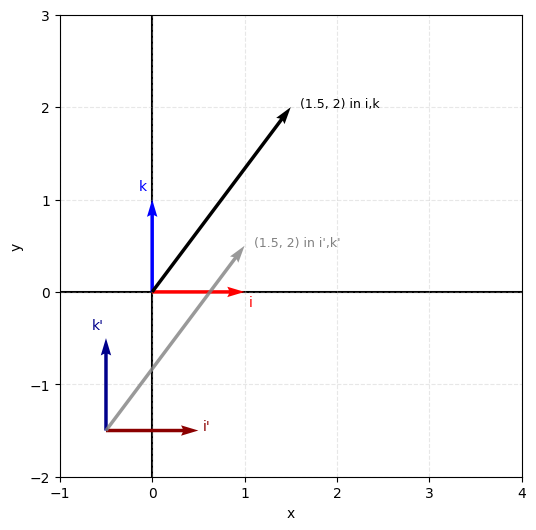
Instead, we can change the coordinate system itself by redefining our basis vectors. The object coordinates (coefficients) stay exactly the same—we're literally warping the space they exist in. For example, instead of our standard basis:

• i = $(1, 0)$
• k = $(0, 1)$

We might create a rotated basis where:

• i' = $(\cos$ (45° rotation)

Now that we've seen how rotation can be achieved by changing our basis vectors, let's explore another fundamental transformation: translation. Translation is simply moving objects from one location to another, but like rotation, we can think of it as a change to our coordinate system itself.

Instead of moving individual objects, we can shift the entire coordinate system by changing where our origin is located. This is like moving the center point from which all measurements are taken.

Consider our standard 2D coordinate system with origin at $(0, 0)$. If we want to translate our scene, we can redefine our coordinate system to have its origin at a different location, say $(-2, -3)$. Now when we specify a point as $(3, 2)$ in our translated coordinate system, it actually appears at in the original world space.

That was a lot to take in! Thankfully, this is all the insight we need to understand linear transformations (translations, rotations, and scaling).

Now that we understand how transformations work conceptually as basis changes, let's explore the mathematical tool that makes these transformations practical: matrices. A matrix is simply a rectangular array of numbers that encodes a linear transformation. Think of it as a compact way to store the instructions for how to transform our coordinate system.

We won't go any deeper into the math, but all you need to know is this beautiful connection: the columns of a transformation matrix are exactly the new basis vectors we want to use.

For a 2×2 matrix in 2D space: $\begin{bmatrix} i'_x & j'_x \\i'_y & j'_y \end{bmatrix}$

Here's where we encounter a fundamental limitation: while 3×3 matrices excel at rotation and scaling, they cannot represent translation. This creates a problem because moving objects is one of the most basic operations we need in 3D graphics.

The elegant solution is to simply add one more dimension and use 4×4 matrices with homogeneous coordinates. By adding this extra dimension to our mathematics, we can represent any combination of translation, rotation, and scaling in a single matrix multiplication! This unification is incredibly powerful because it means we can chain together complex transformations using simple matrix multiplication.

The structure of a 4×4 transformation matrix follows a clear pattern: the upper-left 3×3 section handles rotation and scaling, the rightmost column (excluding the bottom element) handles translation, and the bottom row remains $[0, 0, 0, 1]$ to maintain mathematical consistency.

Thus, our final package looks like this: $[\begin{array}{cccc}{R}_{00}& R_{01}& R_{02}& \end{array}$

We've built a solid theoretical foundation for understanding transformation matrices in 3D graphics. We explored how positions and vectors work in 3D space, learned why matrices are so powerful for coordinate transformations, and discovered why 4×4 matrices are essential for combining rotation and translation operations.

In the upcoming quiz, we'll test your understanding of these transformation concepts and reinforce how matrices work to manipulate objects in 3D space. You'll apply this theoretical knowledge to solve problems involving translation and rotation matrices, solidifying your grasp of how these mathematical concepts create the foundation for 3D graphics transformations.